Título

Los ángulos

 

En el siguiente EVA para ver algunas de las cosas que te pueden facilitar para aprender mejor acerca de los ángulos. Por otra parte podrás ver de una manera mas rápida cuales son los tipos de ángulos, cual es la importancia, ejemplos en la vida diaria y mas.

¿Qué es un ángulo?

Un ángulo es una magnitud que puede ser analizada y comparada con otras. ¿Qué es ángulo? El ángulo es la porción del plano comprendida entre dos semirrectas (lados) con un origen común llamado vértice. Los ángulos parten de un punto y tienen dos líneas que salen desde ese punto y que generan una apertura representada por un arco.

Un ángulo es la parte del plano limitada por dos semirrectas que parten de un mismo punto. Las semirrectas que forman el ángulo se llaman lados y el punto donde se encuentran es el vértice:

Se suelen nombrar con una letra mayúscula en el vértice (A, B, C …) o mediante letras griegas (α, β, γ …).

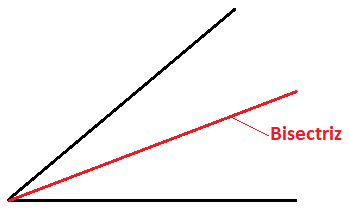
Bisectriz de un ángulo

La bisectriz de un ángulo es la semirrecta que divide al ángulo en dos partes iguales, pasando por el centro. También se puede definir como el lugar geométrico cuyos puntos están a la misma distancia de los lados del ángulo:

Cómo se miden los ángulos

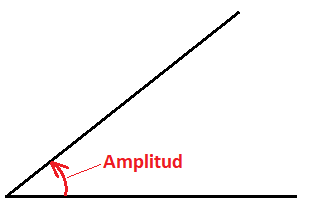
Los ángulos, al no ser figuras cerradas, no se puede medir su área ni su perímetro. Por tanto, cuando hablamos de medida de ángulos nos referimos a su amplitud.

La amplitud de un ángulo es la extensión de plano que ha de recorrer uno de los lados hasta alcanzar la posición del otro, cuando se le hace girar alrededor del vértice:

Por otro lado, la amplitud de un ángulo no depende de la longitud de sus lados. Por ejemplo, en estos dos ángulos, aunque la longitud de sus lados es distinta, la amplitud es la misma:

Para medir los ángulos se utiliza un semicírculo graduado llamado transportador de ángulos:

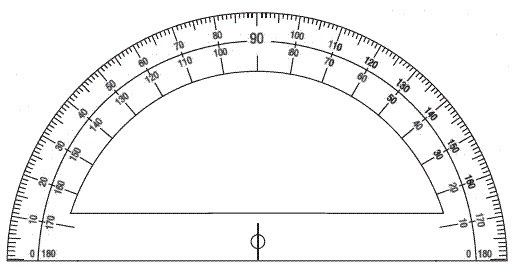
En general, los transportadores de ángulos suelen tener dos escalas, una interior y otra exterior, para medir los ángulos en función de su orientación.

Para medir ángulos con el transportador, se coloca el transportador de manera que uno de los lados del ángulo coincida con la línea horizontal del transportador y el vértice del ángulo coincida con el centro del semicírculo, marcado con una línea vertical. El otro lado del ángulo indicará sobre la graduación del transportador los grados de amplitud del ángulo.

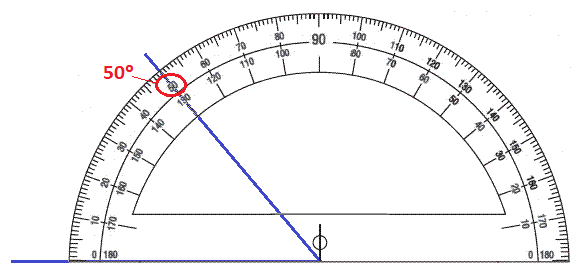
Por ejemplo, en este caso, el ángulo tiene una amplitud de 50º:

Como el ángulo está orientado hacia la derecha, hemos utilizado la escala interior, que es la que empieza en 0º para esa orientación. Si el ángulo estuviera orientado hacia la izquierda, hubiéramos utilizado la escala exterior:

Comúnmente, los ángulos se pueden medir en grados sexagesimales (según el sistema sexagesimal), donde un grado equivale a 60 minutos.

También se pueden medir en grados centesimales, aunque es menos frecuente, donde un grado equivale a 100 minutos.

Tipos de ángulos

Vamos a ver todas las clases de ángulos que existen:

Ángulo agudo

Un ángulo agudo es el que tiene una amplitud menor de 90º:

Ángulo recto

Un ángulo recto es el que tiene una amplitud igual a 90º:

Ángulo obtuso

Un ángulo obtuso es aquel que tiene una amplitud mayor de 90º, pero menor de 180º:

Ángulo llano

Un ángulo llano es el que tiene una amplitud igual a 180º:

Ángulo convexo

Se llama ángulo convexo a todos los ángulos que sean menores de 180º. Todos los ángulos anteriores, a excepción del ángulo llano, son ángulos convexos.

Ángulo cóncavo

Un ángulo cóncavo es aquel que es mayor de 180º pero menor de 360º:

Ángulo completo

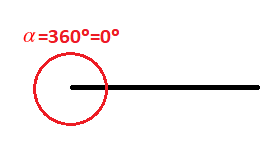
Un ángulo completo es aquel cuyos dos lados coinciden. Su amplitud es de 360º, o de 0º que es lo mismo:

Ángulos iguales

Los ángulos iguales son aquellos que tienen la misma amplitud, es decir, que tienen el mismo número de grados:

Ángulos complementarios

Los ángulos complementarios son aquellos que al sumarlos, el resultado es un ángulo recto, es decir, 90º:

Ángulos suplementarios

Los ángulos suplementarios son los que forman un ángulo llano, es decir, 180º, al sumarlos:

Ángulos adyacentes

Los ángulos adyacentes son ángulos que tienen un vértice y un lado en común. Los ángulos adyacentes suman siempre 180º:

Ángulos consecutivos

Los ángulos consecutivos son aquellos que están colocados uno a continuación de otro, coincidiendo en una de las semirrectas:

Ángulos opuestos por el vértice

Los ángulos opuestos por el vértice son ángulos que tienen el vértice en común y cada uno de sus lados pertenece a la misma semirrecta. Los ángulos opuestos por el vértice son iguales:

Las propiedades de la suma

 

Que son las propiedades de la suma 

Las sumas, tiene diversas propiedades y son las siguientes, las propiedad asociativa, la propiedad conmutativa, el elemento neutro y la propiedad distributiva, las cuales son sirven a nosotros los estudiantes para poder identificas dichas propiedad. 

cual es la importancia 

Estas propiedad son muy importante, debido a que a través de ella nos permite a nosotros diferenciar y saber en qué ámbito y en cuáles momentos podemos usar dichas propiedades. 

cuales son las propiedade y un ejemplo 

Propiedad conmutativa de la suma: cambiar el orden de los sumandos no altera la suma. Por ejemplo, 4 + 2 = 2 + 44+2=2+44, plus, 2, equals, 2, plus, 4.

Propiedad asociativa de la suma: la forma de agrupar los sumandos no cambia la suma. Por ejemplo, (2 + 3) + 4 = 2 + (3 + 4)(2+3)+4=2+(3+4)left parenthesis, 2, plus, 3, right parenthesis, plus, 4, equals, 2, plus, left parenthesis, 3, plus, 4, right parenthesis.

Propiedad de la identidad de la suma: Sumar 000 a cualquier número da por resultado el mismo número. Por ejemplo, 0 + 4 = 40+4=40, plus, 4, equals, 4.

ejercicios practivos 

A continuacion veras los links de algunos videos y poscat para que puedas entender mejor la clase 

Link del poscat educativo 

Link de el entorno virtual de aprendizaje

Más abajo podrás ver un link, el cual accederás para poder activas tus conocimientos prácticas dados en la clase. 

Dale clic aquí para acceder al juego de  conocimientos 

por que es importante la matemática.

                                                                           

"La matemática es la ciencia de estructurar una realidad estudiada, es el conjunto de sus elementos,  proporciones, relaciones y patrones de evolución en condiciones ideales para un ámbito delimitado".

Es decir: "Hacer matemática es desentrañar los ritmos del Universo". (Eso creo, para mis efectos)

Beneficios de las matemáticas para la educación

Por muy soporíferas que puedan parecer, su estudio se traduce en beneficios para la educación y para nuestra vida en general como son los siguientes:

-Ayudan a que tengamos un pensamiento analítico. Lo podríamos definir como el pensamiento dirigido a descomponer los argumentos en sus premisas o expresiones que lo componen, ver las relaciones que hay entre ellas y su conclusión, con el fin de juzgar su veracidad o confiabilidad de la misma. Esto es lo que llevamos a cabo cuando hacemos un problema matemático: recoger los datos, desglosar sus premisas, observar las relaciones que guardan o resolver sistemáticamente sus partes de manera racional.

Las matemáticas están presentes en nuestra vida diaria. Para muchos estudiantes las matemáticas son aburridas, abstractas, carentes de creatividad, complejas y muy difíciles de entender, de ahí las típicas expresiones de “soy de letras” o “lo mío no son los números“.  No obstante, es una asignatura que forma parte del estudio de nuestros hijos y como tal debe de hacerse un esfuerzo para su compresión, y que normalmente conlleva practica constante.

-Las matemáticas desarrollan la capacidad de pensamiento puesto que para encontrar las soluciones, hay que pensar en todo un proceso coherente. Podría decirse que las matemáticas son fundamentales en la educación de los niños, ya que les enseñan a pensar.

-Gracias a las matemáticas podemos explicar cómo funcionan las cosas, es decir, podemos expresar nuestros pensamientos e ideas con claridad, coherencia y precisión. Esto es fundamental y muy positivo para que todos los demás nos comprendan y sepan que somos personas con un pensamiento claro y coherente. Nuestra forma de ordenar ideas y de expresarlas correctamente son gran parte de nuestra imagen.

Aquí mas adelante les mostrare 5 razones para que sepas el porque es importante la matemática

1.- Las matemáticas desarrollan el pensamiento analítico.

Podríamos definirlo como pensamiento dirigido a descomponer los argumentos en las premisas o expresiones que lo componen, observar de manera directa las relaciones que existen entre estos y su conclusión, a fin de juzgar la veracidad o fiabilidad de los mismos.

2.- El pensamiento analítico desarrolla la capacidad de investigar y conocer la verdad sobre el mundo que nos rodea.

Hay verdades que intentamos buscar y que se basan en evidencia objetiva y no en emociones. Ese o esos pensamiento que nos permite estar atentos a los errores, tanto a los de nosotros mismos como a los de los demás, al engaño y a la manipulación es decir falacia.

3.- Las matemáticas fomentan la capacidad de pensar.

Para encontrar soluciones, hay que pensar coherentemente, además de que para los problemas matemáticos existe gran variedad de soluciones.

4.- Gracias a las matemáticas podemos explicar cómo funcionan las cosas.

Con ellas expresamos pensamientos e ideas con claridad, coherencia y precisión. Lo que resulta fundamental y muy positivo para que los demás nos comprendan y sepan que somos personas de pensamiento claro y lógico

5- Las matemáticas aceleran nuestras mentes.

En general, profundizamos nuestro pensamiento al enfrentamos a problemas complejos. Nuestra vida se compone determinantemente por situaciones de elección, enfoque, razonamiento y problemas vitales para los que hay que encontrar soluciones.

Mi Foro

                                             observa detenidamente la imagen y responde:

¿ Por que es necesario el pensamiento divergente y para que nos servirá como futuros maestros?

la mejor manera de aprender matematica

 

La matemática es una ciencia formal que, partiendo de axiomas y siguiendo el razonamiento lógico, estudia las propiedades, estructuras abstractas y relaciones entre entidades abstractas como números, figuras geométricas, iconos, glifos o símbolos en general.

Las matemáticas son el principal elemento para la toma de decisiones, y no solo en temas que tiene que ver en ingenierías o licenciaturas. Estas nos ayudan a reforzar el intelecto, por lo que te invito a perderles el miedo y a estar seguro de que eres bueno en ello; pronto verás excelentes resultados en tus exámenes y en tu vida académica.

“Odio las matemáticas”, “Yo no nací para las matemáticas”, “Las matemáticas son muy difíciles”… ¿Te suenan conocidas esas preguntas y frases? Si respondiste que sí, temo contradecirte: las matemáticas son sumamente fáciles y sobre todo, si las entiendes bien, te llegan a gustar mucho. Por ello te voy a compartir algunos trucos y consejos para que se te facilite el aprendizaje y te enamores de ellas.

• Disfruta tú mismo con las matemáticas.

Para eso necesitas dos ingredientes fundamentales:

Primero: Ama las matemáticas.

Segundo: Dispón de recursos lúdicos y manipulativos que permitan aprender matemáticas de forma natural, gratificante y duradera. Pero te preguntarás… ¿Qué pasa si no me gustan las matemáticas? No te preocupes, ya que si empiezas por el segundo punto te aseguro que amarás las matemáticas.

• Crear ambientes relajados tanto física como emocionalmente.

Es importante tener un lugar de la casa que puede estar compartido con otras funciones (por ejemplo el salón o la cocina) destinado a los materiales o juegos. Cuando hagas alguna propuesta, revisa que el lugar esté despejado y que sea un momento tranquilo, en el que puedas estar presente al 100%. Hay familias a las que les resulta útil fijar un momento del día o de la semana y otras que prefieren ser más espontáneas.

Desprográmate de que no eres bueno o buena para entender las matemáticas y Práctica, práctica y práctica para que ejercite la resolución de problemas. La práctica hace al maestro, es por ello que debes practicarla y en caso de tener dudas pues pregunta al maestro. Mi maestra de la secundaria solía decir ¡Las matemáticas entran por las manos!

Disfrútalas cuando tu maestro te enseñe los temas que involucran las matemáticas. El peor error que podemos cometer es pensar que las matemáticas son difíciles, ya que estamos enfrentándolas con miedo. ¡Atrévete a asumir el reto!

En conclusión, las matemáticas abren las puertas a cálculos y formulaciones abstractas mucho más complejas y permite la expresión por escrito de numerosas relaciones del mundo real. No obstante, nos ayuda a tener pensamiento analítico. Aquí conocimos las diferentes formas, técnicas y métodos para un mejor aprendizaje de las matemáticas, así como también la forma de hacer un hábito y poder aprovechar al máximo dicha asignatura.

Si después de esto, te sientes animado para enfrentar y dominar las matemáticas, no dejes que nada te detenga para estudiar una ingeniería.

para obtener mas información accede a la pagina siguiente matemáticas.